Hilo Cuántico (Pozo delta de Dirac)

$$ -\frac { { \hbar  }^{ 2 } }{ 2m } \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } +0\cdot \psi \left( x \right) =E\psi \left( x \right) $$

Solución:

$$ \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } =-\frac { 2mE }{ { \hbar  }^{ 2 } } \psi \left( x \right) \quad sea\quad { k }^{ 2 }=\frac { 2mE }{ { \hbar  }^{ 2 } }  $$

Organizando:

$$ \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } +{ k }^{ 2 }\psi \left( x \right) =0 $$

Obtenemos una ecuación diferencial de solución armónica cuya solución puede expresarse como combinación lineal de exponenciales complejas o como combinación lineal de senos y coseno de la siguiente forma:

$$ \psi \left( x \right) =A\cdot { e }^{ ikx }+B\cdot { e }^{ -ikx }=A\cdot \cos { \left( kx \right)  } +B\cdot \sin { \left( kx \right)  } \quad con\quad { k }^{ 2 }=\frac { 2mE }{ { \hbar  }^{ 2 } } $$

Partícula bajo potencial constante E>V

La ecuación de Schrödinger esta dada por:

$$ \left( 3 \right) \quad  -\frac { { \hbar  }^{ 2 } }{ 2m } \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } +{ V }_{ o }\cdot \psi \left( x \right) =E\psi \left( x \right)  $$

Solución:

$$ -\frac { { \hbar  }^{ 2 } }{ 2m } \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } =\left( E-{ V }_{ o } \right) \cdot \psi \left( x \right) $$

Organizando:

$$ \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } =-\frac { 2m\left( E-{ V }_{ o } \right)  }{ { \hbar  }^{ 2 } } \cdot \psi \left( x \right) \quad sea\quad { k }^{ 2 }=\frac { 2m\left( E-{ V }_{ o } \right)  }{ { \hbar  }^{ 2 } } $$

$$ \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } +{ k }^{ 2 }\cdot \psi \left( x \right) =0 $$

La solución a esta ecuación es igual a la de la partícula libre por lo que solo difieren en el valor de la frecuencia espacia k.

$$ \left( 4 \right) \quad \psi \left( x \right) =A\cdot { e }^{ ikx }+B\cdot { e }^{ -ikx }=A\cdot \cos { \left( kx \right)  } +B\cdot \sin { \left( kx \right)  } \quad con\quad { k }^{ 2 }=\frac { 2m\left( E-{ V }_{ o } \right)  }{ { \hbar  }^{ 2 } } $$

Partícula bajo potencial constante E<V

La ecuación de Schrödinger esta dada por:

$$ -\frac { { \hbar  }^{ 2 } }{ 2m } \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } +{ V }_{ o }\cdot \psi \left( x \right) =E\psi \left( x \right)  $$

Solución:

$$ -\frac { { \hbar  }^{ 2 } }{ 2m } \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } =\left( E-{ V }_{ o } \right) \cdot \psi \left( x \right) $$

Organizando:

$$ \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } =-\frac { 2m\left( E-{ V }_{ o } \right)  }{ { \hbar  }^{ 2 } } \cdot \psi \left( x \right) \quad sea\quad { k }^{ 2 }=-\frac { 2m\left( E-{ V }_{ o } \right)  }{ { \hbar  }^{ 2 } } $$

Se debe tomar el signo negativo ya que la frecuencia espacial es un número real positivo.

$$ \left( 5 \right) \quad \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } -{ k }^{ 2 }\cdot \psi \left( x \right) =0 $$

Obtenemos una ecuación diferencial cuya solución no es armónica y su solución se expresara como combinación lineal de exponenciales reales de la siguiente forma:

$$ \left( 6 \right) \quad \psi \left( x \right) =A\cdot { e }^{ kx }+B\cdot { e }^{ -kx }\quad con\quad { k }^{ 2 }=\frac { 2m\left( { V }_{ o }-E \right)  }{ { \hbar  }^{ 2 } } $$

A continuación daremos solución a diferentes pozos de potencial, en los cuales se tratara de hallar la función de onda, la energía, los coeficientes de trasmisión y reflexión para el sistema dado según sea el caso.

Hilo Cuántico (Pozo delta de Dirac)

El potencial esta matemáticamente dado por:

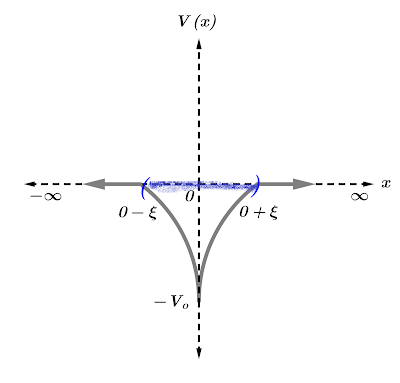
$$V\left( x \right) =-{ V }_{ o }\delta \left( x \right) $$

Gráficamente:

La solución a este potencial se debe realizar considerando una aproximación de borde alrededor del eje y=0, gráficamente esta aproximación estará dada por:

Esta aproximación es mas cercana a algo que físicamente tenga sentido. 

Estados de Ligadura:

El análisis para la región I y III estará descrita por la ecuación de Schrödinger a potencial cero:

$$ -\frac { { \hbar  }^{ 2 } }{ 2m } \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } +0\cdot \psi \left( x \right) =E\psi \left( x \right) $$

Solución:

$$ \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } =-\frac { 2mE }{ { \hbar  }^{ 2 } } \psi \left( x \right) \quad sea\quad { k }^{ 2 }=-\frac { 2mE }{ { \hbar  }^{ 2 } }  $$
Se toma el signo negativo dado a que la energía es menor a cero y el valor de la frecuencia espacial k debe ser un número real positivo. Organizando:

$$ \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } -{ k }^{ 2 }\psi \left( x \right) =0 $$

Obtenemos una ecuación diferencial cuya solución puede expresarse como combinación lineal de exponenciales reales, de la siguiente forma:

$$ \psi \left( x \right) =A\cdot { e }^{ kx }+B\cdot { e }^{ -kx } \quad con\quad { k }^{ 2 }=-\frac { 2mE }{ { \hbar  }^{ 2 } } $$

Solución general en ambas regiones:

$$ \begin{cases} { \psi  }_{ I }\left( x \right) =A\cdot { e }^{ kx }+B\cdot { e }^{ -kx } \\ { \psi  }_{ III }\left( x \right) =A'\cdot { e }^{ kx }+B'\cdot { e }^{ -kx } \end{cases}\quad con\quad { k }^{ 2 }=-\frac { 2mE }{ { \hbar  }^{ 2 } } $$

Al tener un comportamiento de exponenciales reales no se puede hablar de reflexión, trasmisión o incidencia de ondas, por tanto se debe hacer cumplir que las soluciones obtenidas sean soluciones continuas y convergentes, por tanto calculamos los limites al infinito. En la región I debe ser convergente para toda x<0 (-∞) y en la región III debe converger para toda x>0 (∞):

$$ \begin{cases} \lim _{ x\rightarrow -\infty  }{ { \psi  }_{ I }\left( x \right)  } =A\cdot { e }^{ -\infty  }+B\cdot { e }^{ +\infty  }\quad \space \therefore \space B=0. \\ \lim _{ x\rightarrow +\infty  }{ { \psi  }_{ III }\left( x \right)  } =A'\cdot { e }^{ \infty  }+B'\cdot { e }^{ -\infty  }\space \therefore \space A'=0. \end{cases} $$ 

Las soluciones en estas regiones estarán dadas por:

$$ \begin{cases} { \psi  }_{ I }\left( x \right) =A\cdot { e }^{ kx } \\ { \psi  }_{ III }\left( x \right) =B'\cdot { e }^{ -kx } \end{cases}\quad con\quad { k }^{ 2 }=-\frac { 2mE }{ { \hbar  }^{ 2 } }  $$

En la región II nos encontramos con el potencial delta de Dirac, por lo cual la ecuación de Schrödiger queda:

 $$ -\frac { { \hbar  }^{ 2 } }{ 2m } \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } } -{ V }_{ o }\delta \left( x \right) \psi \left( x \right) =E\psi \left( x \right)  $$

Para dar solución a esta ecuación se definirá una vecindad alrededor de x=0, la cual esta dada por:

$$ { B }_{ \xi  }\left( 0 \right) =\left\{ x/\quad |x|<\xi  \right\} \quad con\quad \xi \rightarrow 0 $$

Gráficamente la vecindad puede representarse como:

DAR EXPLICACIÓN DE VECINDAD

Integramos a ambos lados la ecuación de Schrödinger obtenida con limites de vecindad, para ello tenemos:

$$ -\frac { { \hbar  }^{ 2 } }{ 2m } \int _{ -\xi  }^{ \xi  }{ \frac { { d }^{ 2 }\psi \left( x \right)  }{ d{ x }^{ 2 } }  } -{ V }_{ o }\int _{ -\xi  }^{ \xi  }{ \delta \left( x \right) \psi \left( x \right)  } =E\int _{ -\xi  }^{ \xi  }{ \psi \left( x \right)  } $$

Integrando y recordando las propiedades del delta de Dirac actuando sobre una función dentro de una integral tenemos:

$${ -\frac { { \hbar  }^{ 2 } }{ 2m } \frac { { d }\psi \left( x \right)  }{ d{ x } }  }_{ -\xi \rightarrow \xi  }-{ V }_{ o }\psi \left( 0 \right) =E\cdot { \Psi \left( x \right)  }_{ -\xi \rightarrow \xi  }$$

$$ { -\frac { { \hbar  }^{ 2 } }{ 2m } \left( \frac { { d }\psi \left( \xi  \right)  }{ d{ x } } -\frac { { d }\psi \left( -\xi  \right)  }{ d{ x } }  \right)  }-{ V }_{ o }\psi \left( 0 \right) =E\cdot \left( { \Psi \left( \xi  \right) -{ \Psi \left( -\xi  \right)  } } \right) $$

La función mayúscula Psi evaluada en los limites va a dar como resultado cero, dado a que estos limites tienden a cero por tanto su diferencia va a ser nula.

$$ { -\frac { { \hbar  }^{ 2 } }{ 2m } \left( \frac { { d }\psi \left( \xi  \right)  }{ d{ x } } -\frac { { d }\psi \left( -\xi  \right)  }{ d{ x } }  \right)  }-{ V }_{ o }\psi \left( 0 \right) =0 $$

Las derivadas evaluadas en los limites de la vecindad corresponden a la función...

$$ { \left( \frac { { d }{ \psi  }_{ III }\left( \xi  \right)  }{ d{ x } } -\frac { { d }{ \psi  }_{ I }\left( -\xi  \right)  }{ d{ x } }  \right)  }=-\frac { { 2mV }_{ o } }{ { \hbar  }^{ 2 } } { \psi  }_{ II }\left( 0 \right) $$

$$ { kB'\cdot { e }^{ -k\xi  }+kA\cdot { e }^{ -k\xi  } }=\frac { { 2mV }_{ o } }{ { \hbar  }^{ 2 } } { \psi  }_{ II }\left( 0 \right) $$

$$ { kB'\cdot { e }^{ k\xi  }+kA\cdot { e }^{ k\xi  } }=\frac { { 2mV }_{ o } }{ { \hbar  }^{ 2 } } A{ e }^{ 0 } $$